Həndəsi silsilə

Həndəsi silsilə (bəzən həndəsi ardıcıllıq) — ilk həddi sıfırdan fərqli olmaqla ikincidən başlayaraq hər bir həddi özündən əvvəlki ilə silsilə vuruğu adlanan sıfırdan fərqli sabit ədədin hasilinə bərabər olan ədədi ardıcıllıq.^[1] Məsələn, 2, 6, 18, 54, … ardıcıllığı silsilə vuruğu 3 olan həndəsi silsilədir. Eynilə 10, 5, 2.5, 1.25, … silsilə vuruğu 1/2 olan həndəsi silsilədir. Həndəsi silsiləyə misal olaraq 2^k və 3^k kimi sıfırdan fərqli r sabitinin r^k qüvvətlərini göstərmək olar. Həndəsi silsilənin ümumi forması belədir

$a,\ ar,\ ar^{2},\ ar^{3},\ ar^{4},\ \ldots$

burada r ≠ 0 silsilə vuruğu, a ≠ 0 isə ardıcıllığın başlanğıc qiymətinə bərabər olan əmsaldır.

Silsilə və sıra arasındakı arasındakı fərq ondan ibarətdir ki, silsilə ardıcıllıq, sıra isə cəmdir.

Elementar xassələr redaktə

İlk həddi a = a₁, silsilə vuruğu r olan həndəsi silsilənin n-ci həddi aşağıdakı kimi verilir:

$a_{n}=a\,r^{n-1}$

Belə həndəsi silsilə rekurrent münasibətə uyğundur:

hər bir $n\geq 2$ tam ədədi üçün $a_{n}=r\,a_{n-1}$

Ümumiyyətlə, verilmiş ardıcıllığın həndəsi olub-olmadığını yoxlamaq üçün sadəcə ardıcıllığın bütün hədlərinin eyni silsilə vuruğuna malik olub-olmadığını yoxlamaq kifayətdir.

Silsilə vuruğu mənfi olarsa, işarəsi müsbət və mənfinin arasında dəyişən ədədi ardıcıllıq alınar. Misal üçün

1, −3, 9, −27, 81, −243, …

silsilə vuruğu −3 olan həndəsi silsilədir.

Həndəsi silsilənin davranışı silsilə vuruğunun qiymətindən asılıdır.

Silsilə vuruğu:

müsbətdirsə, bütün hədlərin işarəsi ilk həddinki ilə eyni olacaq.
mənfidirsə, hədlər müsbət və mənfi arasında dəyişəcək.
1-dən böyükdürsə, müsbət və ya mənfi sonsuzluğa doğru eksponensial (üstlü şəkildə) artacaq (ilk həddin işarəsindən asılı olaraq).
1 olduqda, silsilə sabit ardıcıllıqdır.
−1 ilə 1 arasında olduqda, lakin sıfır qiymətini almadıqda, ardıcıllıq sıfıra doğru (→ 0) eksponensial dağılacaq.
−1 olduqda, ardıcıllığın hər bir həddi mütləq qiymətcə sabitdir və hədlərin işarəsi növbə ilə dəyişir.
−1-dən kiçik olduqda, mütləq qiymətlər üçün işarə növbə ilə dəyişdiyinə görə (işarəsiz) sonsuzluğa doğru eksponensial artım var.

Həndəsi silsilələr (silsilə vuruğu −1, 1 və ya 0-dan fərqli olan) 4, 15, 26, 37, 48, … (silsilə fərqi 11-dir) kimi ədədi silsilənin xətti artımından (və ya azalmasından) fərqli olaraq eksponensial artım və ya eksponensial dağılma nümayiş etdirir. Bu nəticə T.R. Maltus tərəfindən Populyasiya prinsipinin riyazi təməli kimi qəbul edilib.^[2] Qeyd etmək lazımdır ki, iki növ silsilə bir-birilə bağlıdır: ədədi silsilənin hər bir həddini qüvvətə yüksəltmək həndəsi silsiləni, müsbət silsilə vuruğuna malik həndəsi silsilənin hər bir həddini loqarifmləmək ədədi silsiləni verir.

Həndəsi silsilənin tərifinin maraqlı nəticəsi ondan ibarətdir ki, hər hansı üç ardıcıl a, b və c hədləri aşağıdakı tənliyi ödəyəcəkdir:

$b^{2}=ac$

burada b, a və c ədədlərinin həndəsi ortasıdır.

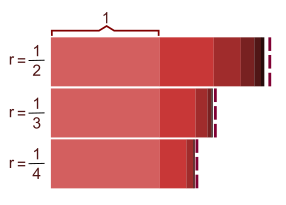
Tarix redaktə

Mesopotamiyanın erkən xanədanlıq dövrünə aid gil lövhədə əsası 3, vuruğu 1/2 olan həndəsi silsilədən bəhs edilir. Bunun Şuruppak şəhərindən olan şumerlərə aid olduğu irəli sürülür. Bu, Babil riyaziyyatı dövründən əvvələ aid həndəsi silsilə ilə haqqındakı yeganə məlum qeyddir.^[3]

Evklidin Başlanğıclarının VIII və IX kitablarında həndəsi silsilələr (məsələn, ikinin qüvvətləri) təhlil edilir və onların bir neçə xassəsi verilir.^[4]

İstinadlar redaktə

↑ Hall & Knight, Higher Algebra, p. 39, ISBN 81-8116-000-2
↑ Malthus T.R. 1798. An Essay on the Principle of Population. Oxford World's Classics reprint.
↑ Friberg, Jöran (2007). "MS 3047: An Old Sumerian Metro-Mathematical Table Text". In Friberg, Jöran (ed.). A remarkable collection of Babylonian mathematical texts. Sources and Studies in the History of Mathematics and Physical Sciences. New York: Springer. pp. 150–153. doi:10.1007/978-0-387-48977-3. ISBN 978-0-387-34543-7. MR 2333050 Arxivləşdirilib 2023-07-22 at the Wayback Machine.
↑ Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.). New York: Dover Publications.

[1] Hall & Knight, Higher Algebra, p. 39, ISBN 81-8116-000-2

[2] Malthus T.R. 1798. An Essay on the Principle of Population. Oxford World's Classics reprint.

[3] Friberg, Jöran (2007). "MS 3047: An Old Sumerian Metro-Mathematical Table Text". In Friberg, Jöran (ed.). A remarkable collection of Babylonian mathematical texts. Sources and Studies in the History of Mathematics and Physical Sciences. New York: Springer. pp. 150–153. doi:10.1007/978-0-387-48977-3. ISBN 978-0-387-34543-7. MR 2333050 Arxivləşdirilib 2023-07-22 at the Wayback Machine.

[4] Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.). New York: Dover Publications.

[1]

[2]

[3]

[4]