Vikipediya

Monti Holl problemi

Monti Hall problemi — Amerika istehsalı olan "Let's Make a Deal" (azərb. "Gəlin razılaşaq"‎) adlı və daha sonra aparıcın şərəfinə "Monty Hall" (azərb. "Monti Hall"‎) adlandırılmış oyun şousunda irəli sürülən ehtimal problemi formasında beyin yoran tapmacadır. Bu problem 1975-ci ildə Stiv Selvin tərəfindən "The American Statistician" (azərb. "Amerikalı Statist"‎) jurnalına göndərdiyi məktubda izah (həll) edilmişdir. Bu, 1990-cı ildə "Parade" jurnalındakı Meriln vos Savantın "Ask Marilyn" (azərb. "Merilndan soruş"‎) bölməsində sitat kimi verilmiş oxucu məktubundan götürülmüş bir sual kimi məşhurlaşmışdır:

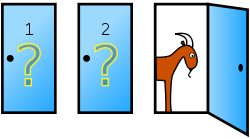
Yeni maşına sahib olmaq məqsədi ilə iştirakçı bir qapı seçir, məsələn, bu nümunədə 1 nömrəli qapı. Daha sonra veriliş aparıcısı digər qapılardan birini - məsələn, bu nümunədə 3 nömrəli qapını açaraq qapı arxasındakı keçini aşkara çıxarmaqla iştirakçıya seçimini 1 nömrəli qapıdan 2 nömrəli qapıya dəyişməyi və ya əvvəlki qərarında qalmağı təklif edir.
" Təsəvvür edin ki, oyun şousundasınız və sizə seçim haqqı kimi üç qapı təqdim olunmuşdur: Bir qapının arxasında maşın, digər iki qapının arxasında isə keçilər vardır. Siz bir qapı seçmirsiniz, məsələn 1 nömrəli qapı. Daha sonra hər bir qapının arxasında nəyin olduğunu əvvəlcədən bilən veriliş aparıcısı digər iki qapıdan birini açır, məsələn 3 nömrəli qapı. Ardınca isə o, sizdən soruşur: "Seçiminizi 2 nömrəli qapıya dəyişmək istəyirsinizmi?" Bu vəziyyətdə seçiminizi dəyişmək sizin üçün sərfəlidirmi? "

Vos Savantın cavabına görə iştirakçı öz seçimini dəyişərək digər qapını seçməlidir. Standart fərziyyələrə əsasən seçimini dəyişən iştirakçıların maşın qazanma şansı 2/3 olarkən öz əvvəlki seçimlərində sabit qalan iştirakçıların bu uduşu qazanma şansı yalnızca 1/3-dir.

Təqdim olunmuş ehtimallar aparıcı və iştirakçının qapıları necə seçəcəyinə əsaslanan xüsusi fərziyyələrdən asılıdır. Burada (bu standart şərtlər altında) həlledici məqam iştirakçının ən başda 1 nömrəli qapını seçdiyi zamanla müqayisədə indi 2 və 3 nömrəli qapılar haqqında daha çox məlumat vardır: aparıcının məqsədli şəkildə edilmiş hərəkəti iştirakçının seçmədiyi qapıya əlavə dəyər əlavə edir, lakin iştirakçının ən başda seçdiyi qapının dəyərini dəyişmir. Bu məsələyə təsir edən digər bir yanaşma isə iştirakçının seçimini dəyişdirməsinin bu iki qapı arasında təsadüfi seçim etməsindən daha fərqli bir hərəkət olduğunu irəli sürür. Yəni, adıçəkilən birinci hadisə baş verərkən iştirakçı əvvəlki məlumata əsaslanaraq bu qərarı verir, lakin ikinci hadisəni seçərkən o, bunu etmir. Təsvir olunan davranışlardan başqa digər mümkün davranışlar iştirakçının əlavə ya əlavə informasiya ilə təmin edə bilər, ya da məsələyə heç bir təsir göstərməz və beləliklə, müxtəlif ehtimallar meydana gətirər. Burada digər bir məqam isə sizin qapı seçiminizi dəyişməklə maşın qazanmaq şansınızın birbaşa ilk seçimizdə uduşlu qapını seçmə şansınızla əlaqali olmasıdır: əgər siz ilk cəhdinizdə doğru seçim etmisinizsə, bu zaman seçiminizi dəyişmək sizin məğlubiyyətinizlə; yox, əgər siz ilk seçimizdə yanlış qapını seçmisinizsə, seçiminizi dəyişmək sizin yarışmada qalib gəlməyinizlə nəticələnəcək. Belə ki, sizin ilk cəhdinizdə doğru qapını seçmə ehtimalınız 1/3, səhv qapını seçmə ehtimalınız isə 2/3-dir.

Bir çox oxucu Savantın izahına baxmayaraq iştirakçının seçimini dəyişməsinin uğurlu bir qərar olmasına etiraz etdi. "Parade" jurnalında bu problem nəşr edildikdən sonra 10000-ə yaxın oxucu, o cümlədən təqribən 1000 fəlsəfə doktoru jurnala məktub yazdı və onların əksər hissəsi Savantın səhv fikirdə olduğunu iddia edirdi. Hətta verilən izahlar, simulyasiyalar və əvvəlki riyazi isbatlara baxmayaraq hal-hazırda da bir çox insan iştirakçının seçimini dəyişməsinin ən yaxşı strategiya olduğunu qəbul etmir. Tarixdə riyaziyyat sahəsində ən çox töhfə vermiş alimlərdən biri olan Pal Erdöş də ona Savantın proqnozlaşdırdığı nəticə kompüter simulyasiyası ilə göstərilənə qədər bu həllə şübhə ilə yanaşırdı.

Bu problem həqiqətə uyğun paradoksdur. Doğru seçim (yəni, iştirakçının seçdiyi qapını dəyişməsi) ümumi mənada düşünülənlərə əks olduğun üçün absurd görünə bilər, lakin buna baxmayaraq həm də əyani sürətdə doğrudur. "Monti Hall" problemi daha əvvəlki illərdə meydana çıxan "Üç məhbus" problemi və daha yaxın zamanda irəli sürülən "Bertrandın qutusu" paradoksu ilə riyazi cəhətdən yaxından əlaqəlidir.

Paradoks

redaktə

Stiv Selvin 1975-ci ildə "Let's Make a Deal" adlı oyun şousuna əsaslanan problemi təsvir edən məktub yazaraq "American Statistician" jurnalına göndərdi və sonrakı nəktubunda isə bunu "Monti Hall" problemi adlandırdı. Bu problem Martin Qardnerin 1959-cu ildə "Scientific American" jurnalında qələmə aldığı "Riyaziyi oyunlar" mövzusuna daxil olan "Üç məhbus" problemi və həmçinin Qardnerin kitabı olan "Aha Gotcha"da təsvir etdiyi "Üç qabıq" problemi ilə riyazi cəhətdən eynidir.

Eyni problem 19990-cı ildə Kreq Videkr tərəfindən "Parade" jurnalındakı Meriln vos Savantın "Ask Marilyn" hissəsinə ünvanladığı məktubda yenidən qeyd olunmuşdu:

  Təsəvvür edin ki, oyun şousundasınız və sizə seçim haqqı kimi üç qapı təqdim olunmuşdur: Bir qapının arxasında maşın, digər iki qapının arxasında isə keçilər vardır. Siz bir qapı seçmirsiniz, məsələn 1 nömrəli qapı. Daha sonra hər bir qapının arxasında nəyin olduğunu əvvəlcədən bilən veriliş aparıcısı digər iki qapıdan birini açır, məsələn 3 nömrəli qapı. Ardınca isə o, sizdən soruşur: "Seçiminizi 2 nömrəli qapıya dəyişmək istəyirsinizmi?" Bu vəziyyətdə seçiminizi dəyişmək sizin üçün sərfəlidirmi?  

Standart fərziyyələr

redaktə

Standart fərziyyələrə əsasən maşın qazanma ehtimalı iştirakçı öz seçimini dəyişdikdən sonra 2/3-yə bərabərdir. Bu həll üçün əsas məqam aparıcının davranışıdır. Sualın "Parade" jurnalına göndərilmiş verisyasındakı qeyri-müəyyənliklər aparıcının davranışları ilə bağlı protokolu açıq-aşkar müəyyənləşdirmir. Halbuki Kreqin sualı ilə birgə çap olunmuş Merilnin həlli bunu aydın formada ifadə edir və həm Selvin, həm də Savat aparıcının bu şoudakı rolunu aşağıdakı kimi açıq-aydın müəyyənləşdirir:

  1. Aparıcı hər zaman iştirakçı tərəfindən seçilməyən qapılardan birini açmalıdır.
  2. Aparıcın açacağı qapının arxasında hər zaman keçi olmalıdır, maşın yox.
  3. Aparıcı qapını açdıqdan sonra hər zaman iştirakçıya seçimini dəyişmək və ya əvvəl seçdiyi qapıda qalmaq fürsətini təqdim etməlidir.

Bu fərziyyələrdən hər hansı biri dəyişərsə, bu zaman iştirakçının öz qapı seçimini dəyişməklə maşın qazanma ehtimalı da fərqli ola bilər. Həmçinin bunu da əlavə etmək lazımdır ki, maşın təsadüfi şəkildə qapılardan birinin arxasına yerləşdirilir və əgər iştirakçı ən başda maşın olan qapını seçərsə, onda aparıcı arxasında keçinin olduğu digər iki qapıdan təsadüfi şəkildə birini aça bilər. Bəzi müəlliflər iştirakçının ilk seçiminin də, həmçinin təsadüf olduğunu güman edirlər.

Sadə həllər

redaktə
 
Oyunun üç mümkün forması: bunlardan ikisində iştirakçı bir qapı açılmazdan əvvəl seçdiyi qapını dəyişməklə uduş qazanır.

"Parade" jurnalında vos Savant tərəfindən təqdim edilmiş həll üç qapı arxasındakı bir maşın və iki keçinin üç mümkün qoyuluşunu və hər vəziyyətdə ən başda 1 nömrəli qapını seçdikdən sonra bu seçimdə qalmağın və ya dəyişməyin nəticələrini göstərir:

1 nömrəli qapının arxasında 2 nömrəli qapının arxasında 3 nömrəli qapının arxasında 1 nömrəli qapıda qalan zaman nəticə Qapı seçimini dəyişməklə əldə olunan nəticə
Keçi Keçi Maşın Keçi qazanır Maşın qazanır
Keçi Maşın Keçi Keçi qazanır Maşın qazanır
Maşın Keçi Keçi Maşın qazanır Keçi qazanır

Əvvəlki seçimində qalan iştirakçı üç ehtimaldan yalnızca birində qalib gəlir, lakin aparıcı arxasında keçi olan qapını açdıqdan sonra qapı seçimini dəyişərsə bu üç ehtimaldan ikisində qalib gələr.

İntuitiv izahda qeyd olunur ki, əgər iştirakçı əvvəlcə keçi olan qapını seçərsə (3 qapıdan 2-də bu mümkündür), o, seçimini dəyişməklə maşın qazanacaq, çünki artıq keçi seçilə bilməz. Halbuki əgər iştirakçı əvvəlki seçimində qapını seçmiş olarsa, o, seçimini dəyişməklə maşın qazana bilməyəcək. Aparıcının daha sonr0 arxasında keçi olan seçilməmiş qapılardan birini açması faktı əvvəlki ehtimala təsir etmir və onu dəyişmir.

Əksər insanlar iştirakçının seçimini dəyişməsinin burada bir əhəmiyyət kəsmədiyi nəticəsinə gəlir, çünki iki qapı, bir maşın var və uduş şansı 50%-dir. Bu, aparıcının qapını təsadüfi olaraq açması halı üçün xarakterikdir, lakin burada məsələ belə deyildir; açılan qapı iştirakçının əvvəlki seçimindən asılıdır, belə ki, asılılıq olmaması fərziyyəsi buraya uyğun deyildir. Aparıcı qapını açmazdan əvvəl maşının hər qapının arxasında olması ehtimalı 1/3-dir. Əgər maşın 1 nömrəli qapının arxasındadırsa, aparıcı 2 və ya 3 nömrəli qapının aça bilər, beləliklə, maşın 1 nömrəli qapının arxasında olarsa və aparıcı 3 nömrəli qapının açarsa, bu zaman ehtimal 1/3 x 1/2 = 1/6-dir. Halbuki əgər maşın iki nömrəli qapının arxasında olarsa (iştirakçı 1 nömrəli qapını seçmişdir), aparıcı məcburən 3 nömrəli qapını açmalıdır və bu da ehtimalın 1/3 x 1 = 1/3-ə bərabər olması mənasına gəlir. Bunlar aparıcının 3 nömrəli qapını açmasının iki mümkün halıdır, belə ki, əgər iştirakçı 1 nömrəli qapını seçmişdirsə və aparıcı 3 nömrəli qapının açırsa, maşının 2 nöçrəli qapının arxasında olması ehtimalı 1 nömrəli qapının arxasında olması ehtimalından 2 dəfə çoxdur.

 
Maşının seçilən qapı arxasında olması ehtimalı 1/3, digər iki qapıdan birinin arxasında olması ehtimalı isə 2/3-dir.
 
Aparıcı qapını açır, digər iki qapı üçün olan birgə ehtimal dəyişməz olaraq 1/3-də qalır, lakin açılan qapı üçün bu, 0-a bərabər olur.

Həlli başa düşməyin digər bir yolu isə əvvəlcədən seçilməyən iki qapının birgə hesaba alınmasıdır. Sisl Adamsın irəli sürdüyü kimi, "Monti itirakçıya qarşılıq verərək deyir: siz əvvəlcə seçdiyiniz qapıda qala bilərsiniz və ya siz digər iki qapını seçə bilərsiniz". Maşının digər iki qapının arxasında olması vəziyyətində iştirakçının maşın qazanma ehtimalı, yəni 2/3 Monti tərəfindən qapılardan biri açıldıqdan sonra da dəyişmir, çünki maşının olduğu yeri əvvəlcədən bilərək onun tək məqsədi keçinlərdən birini aşkara çıxarmaqdır. Beləliklə, iştirakçının aparıcının qapılardan birini açmasından sonrakı seçimi aparıcının iştirakçıya qapını əvvəlki seçimindən digər iki qapıya dəyişməsini təklif etməsindən fərqli deyildir. Bu halda dəyişmək açıq-aşkar iştirakçıya maşın qazanmaq üçün 2/3-yə bərabər ehtimal təklif edir.

Kit Devlinin dediyi kimi, "Monti qapını açmaqla iştirakçıya "Seçmədiyiniz iki qapı var və uduşun onlardan birinin arxasında olması ehtimalı 2/3-yə bərabərdir. Mən digər iki qapıdan birini açaraq sizə həmin qapının arxasında maşın olmadığını göstərməklə yardım edəcəyəm. Siz indi bu əlavə informasiyadan istifadə edərək seçim edə bilərsiniz. Sizin 1 nömrəli qapını seçməklə uduş qazanmaq ehtimalınız 1/3-dir. Mən bunu dəyişmədim, lakin 3 nömrəli qapını açmaqla sizin seçiminizi dəyişərək 2 nömrəli qapını seçməklə uduş qazanma ehtimalınızın 2/3 olduğunu göstərdim." deyir."

Vos Savant və mətbuatın qəzəbi

redaktə

Vos Savant "Monti Hall" problemi ilə bağlı qeydlərində iştirakçının seçimini dəyişməli olduğunu yazmışdı. O, oxucularından minlərlə məktub aldı və əksər insanlar onun cavabı ilə razılaşmadılar. 1990-1991-ci illər ərzində "Parade" jurnalında onun paradoksa həsr olunan daha üç qeydi çap olundu. Vos Savantın oxucularıdnan qəbul edilmiş çoxsaylı məktublar Donald Qranberq tərəfindən qələmə alınan "Monti Hall" Dilemması: Beyinlə bağlı mükəmməl illüziyakitabında nəşr olunmuşdur. Müzakirə digər qəzet və jurnallara da yayıldı (məsələn, Sisl Adamsın "The Straight Dope"qəzetindəki qeydlərində və "The New York Times" qəzetində).

Cavabını aydınlaşdırmaq üçün Savant "Üç qabıq" problemini irəli sürdü: "Siz kənara baxırsınız və mən bu üç qabıqdan birinə noxud dənəsi qoyuram. Daha sonra sizdən bir qabıq seçməyinizi xahiş edirəm və bu zaman sizin doğru qabığı seçmə ehtimalınız 1/3-dir, razılaşırsınızmı? Ardınca isə mən digər iki qabıqdan altında noxud dənəsi olmayanı qaldırıram. Seçdiyinizin nə olduğundan asılı olmayaraq bunu edə biləcəyimdən (və edəcəyimdən) biz sizin seçdiyiniz qabıq üzərindəki ehtimalları yoxlamaq üçün bizə yardım edəcək heç bir şey öyrənmədik". O, həmçinin buna bənzər simulyasiyanı üç kartla da etmişdir.

İstifadə olunan ədəbiyyat

redaktə

Xarici keçidlər

redaktə
Mənbə — "https://az.wikipedia.org/w/index.php?title=Monti_Holl_problemi&oldid=7242483"