Tənbölən
Tənbölən (lat. bi- "ikiqat" və sectio "bölmə") və ya "bucağın tənböləni" — başlanğıcı bucağın təpəsində olan və onu iki bərabər bucağa ayıran parçaya deyilir. Tənböləni bucağın daxilində yerləşən və onun tərəflərindən eyni uzaqlıqda olan nöqtələrin həndəsi yeri kimi də təyin etmək olar.
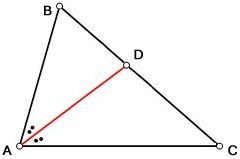
Üçbucağın təpəsini onun qarşı tərəfi ilə birləşdirən və bu təpədəkı bucağı yarıya bölən parçaya üçbucağın tənböləni deyilir.
Üçbucağın üç tənböləni var.
Bərabəryanlı üçbucağın xassələri
redaktə- Üçbucağın iki tənböləni bərabərdirsə, onda üçbucaq bərabəryanlıdır və digər tənböləni həm üçbucağın medianı, həm də hündürlüyüdür. Bunun tərsi də doğrudur: bərabəryanlı üçbucağın iki tənböləni bərabər, üçüncü tənböləni isə həm medianı, həm də hündürlüyüdür.
- Bərabərtərfli üçbucağın hər üç tənböləni bərabərdir.
- Bərabərtərəfli üçbucağın hər üç xarici bucağının tənböləni qarşı tərəfə paraleldir.
Üçbucağın tənböləni
redaktə.
- , burada - yarımperimetrdir.
Uzunluğu uyğun olaraq və , olan A, B və C bucaqlarının tənbölənləri üçün ağağıdakı doğrudur:[1]
- ,
- ,
- Üçbucağın daxili tənbölənlərin kəsişmə nöqtəsi bucağının tənbölənini nisbətdə bolür, burada , , — üçbucağın tərəflridir,
- — uyğun olaraq təpəsinin qarşısındakı tərəf,
- — uyğun olaraq təpəsindəki bucaq,
- — tərəfinə çəkilmiş hündürlük.
- — tərəfinə çəkilmiş daxili tənbölən,
- — daxili tənböləninin tərəfini böldüyü parçaların uzunluqları,
- — təpəsindən tərəfinin uzantısına çəkilmiş xarici tənböləninin uzunluğu.
- — xarici tənböləninin tərəfinin uzantısı ilə kəsişmə nöqtəsini də özündə saxlayan parçanin bölündüyü hissələrin uzunluqlarıdır.
Xarici keçidlər
redaktə- ↑ Simons, Stuart. Mathematical Gazette 93, March 2009, 115-116.